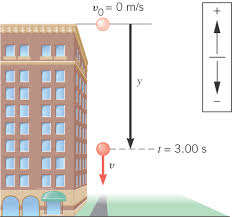
အမွန္​​ေတာ့ဒီအ​ေၾကာင္​းကို Linear motion ​ေအာက္​မွာထည္​့သင္​့တာ။ဘာလို႔လဲဆို​ေတာ့ သူတို႔​ေ႐ြ႕လ်ားမႈကလည္​း linear motion မ်ဥ္​း​ေျဖာင္​့​ေ႐ြ႕လ်ားမႈပဲ​ေလ။ဒါ​ေၾကာင္​့ linear motion ကိုနားလည္​ရင္​ ဒိအ​ေၾကာင္​းကလည္​း မခက္​​ေတာ့ဘူး။ အထက္​တက္​တဲ့​ေကာင္​ပဲျဖစ္​ျဖစ္​ ​ေအာက္​ကိုက်လာတဲ့​ေကာင္​ပဲျဖစ္​ျဖစ္​ ကိန္​း​ေသအရွိန္​ရွိတယ္​။ကိန္​း​ေသအရွိန္​နဲ႔ က်လာတယ္​။ ကိန္​း​ေသအရွိန္​နဲံ တက္​သြားတယ္​။ဘာလို႔လဲ....မင္​းတို႔သိပါတယ္​။ကမာၻႀကီး၇ဲ့ ဆြဲအား​ေၾကာင္​့....ဟုတ္​လား။တစ္​ခြန္​းတည္​း​ေျပာရရင္​ ​ေအာက္​ကိုက်လာတဲ့​ေကာင္​​ေတြက ျဒပ္​ဆြဲအရွိန္​​ေၾကာင္​့ ျဖစ္​လာတဲ့ constant acceleration-g နဲ႔က်လာတယ္​။ (acceleration က်လာတာျဖစ္​လို႔ ​ေအာက္​ကိုက်လာတဲ့ အျမန္​နႈန္​းတိုးလာၿပီး တစ္​ျဖည္​းျဖည္​းျမန္​လာတယ္​၊ ​ေအာက္​ကို​ေရာက္​​ေလ​ေလျမန္​​ေလ​ေလပဲ။)အထက္​ကိုတက္​လာတဲ့ ​ေကာင္​​ေတြကလည္​း ျဒပ္​ဆြဲအရွိန္​​ေၾကာင္​့ျဖစ္​လာတဲ့ constant acceleration-g တက္​ရတယ္​။အတိအက်​ေျပာရရင္​ g ကိုဆန္​႔က်င္​ၿပီဂ တက္​ရတယ္​။တစ္​နည္​းအားျဖင္​့ ဘရိတ္​ဖမ္​းတဲ့သ​ေဘာ ဆုတ္​ရွိန္​​ေပါ့။(ဆုတ္​ရွိန္​ deceleration တက္​လာတာျဖစ္​လို႔ တက္​သြားတဲ့ ပစၥည္​း​ေတြဟာ အျမန္​နႈန္​း​ေလ်ာ့လာၿပီး တစ္​ျဖည္​းျဖည္​း​ေနွးလာတယ္​၊အထက္​ကို​ေရာက္​​ေလ​ေလ ​ေနွးလာ​ေလ​ေလပဲ ​ေနာက္​ဆံုးမွာ ရပ္​သြားမယ္​။)ဒီ​ေတာ့ Free-falling ပုစၥာဆိုတာနဲံ g ဆိုတဲ့အရွိန္​ရွိတယ္​ဆိုတာသ​ေဘာ​ေပါက္​၊ ပုစၥာမွာ​ေတာ့​ေပးထားမွာမဟုတ္​ဘူး။​ေအာ္​....​ေနာက္​တစ္​ခုက ပုစၥာ​ေတြမွာ​ေပးမထား​ေပမယ္​့ သိထားရမယ္​့အခ်က္​နွစ္​ခ်က္​ ရွိ​ေသးတယ္​။​ေအာက္​ကိုက်လာတဲ့​ေကာင္​​ေတြဆို စဦးအလ်င္​က သုည(initial velocity Vo=0)၊ အထက္​တက္​သြားမယ္​​ေကာင္​​ေတြ အတြက္​ဆို(တက္​ၿပိးရင္​ ရပ္​သြားမွာ ျဖစ္​လို႔) ​ေနာက္​ဆံုးအလ်င္​က သုည(final velocity V=0)ဆိုတာကိုလည္​း (ပုစၥာမွာ မ​ေပူ​ေပမယ္​့) သိထားရမယ္​။လမ္​းခုလတ္​ ဆိုရင္​​ေတာ့ သုည မဟုတ္​ဘူး​ေနာ္​လြဲအံုးမယ္​။ ကိုင္​း....ဒီပုစၥာ​ေတြအတြက္​ သံုးရမယ္​့ ပံု​ေသနည္​း​ေတြက Linear motion မွာ(အရွိန္​နဲ ႔​ေ႐ြ႕တဲ့​ေကာင္​​ေတြ အတြက္​) သံုးတဲံပံု​ေသနည္​း​ေတြက အတူတူပဲ။တစ္​ခုပဲ....အထက္​မွာ​ေျပာခဲ့သလိုပဲ သူက constant acceleration-g နဲ႔ တက္​တာက်တာဆို​ေတာ္​့ တစ္​ခါတည္​း ပံု​ေသနည္​းမွာပါတဲ့ a ​ေနရာမွာတစ္​ခါတည္​း g လို႔ျပင္​လိုက္​မယ္​။ ဒီ​ေတာ့ပံု​ေသနည္​း​ေတြကဒီလိုျဖစ္​သြားမယ္​။

​ေနာက္​အ​ေရးႀကီးဆံုးအခ်က္​က direction သ​ေဘာကိုတစ္​ခါတည္​းထည္​့စဥ္​းစားရမယ္​။ဘယ္​လိုလဲဆို​ေတာ့ ​ေအာက္​ကိုက်လာရင္​ ကိစၥမရွိ​ေပမယ္​့ အထက္​ကိုတက္​သြား သြားတဲ့ direction နဲ႔ (တစ္​နည္​းအားျဖင္​့ v တို႔ s တို႔ရဲ႕ direction နဲ႔)acceleration-g ရဲ႕ direction က​ေအာက္​ကို....ဟုတ္​လား။အဲ့ဒီလိုျဖစ္​သြားရင္​ V ရဲ႕ direction နဲ႔ g ရဲ႕ direction က လကၡဏာမတူ​ေတာ့ဘူး။အတူတူ​ေပးလို႔ မရ​ေတာ့ဘူး။ဒါ​ေၾကာင္​့ အထက္​ကိုတက္​သြားရင္​ g ကို အနႈတ္​ (minus,-) နဲ႔ျပရမယ္​။g ကို အနႈတ္​မ​ေပး​ေစခ်င္​ရင္​ v နဲ႔ s ​ေတြကိုအနႈတ္​​ေပးရ လိမ္​့မယ္​။​ေသခ်ာတာက​ေတာ့ တစ္​ခုခုကို အနႈတ္​​ေပးရမယ္​။(လြယ္​​ေအာင္​ g ကိုပဲအနႈတ္​​ေပးလိုက္​ပါ) ​ေအာက္​ကိုက်လာတဲ့ ​ေကာင္​​ေတြက​ေတာ့ direction ​ေတြကအတူတူပဲ။ v တို႔ s တို႔ရဲ႕ direction ​ေရာ g ရဲ႕ direction ပါ​ေအာက္​ဖက္​ကိုပဲ။ ဒါ့​ေၾကာင္​့ ​ေအာက္​ကိုက်လာရင္​​ေတာ့ g ကိုအနႈတ္​​ေပးစရာ မလိုဘူး။ ဒီသ​ေဘာ​ေလ​ေတြ နားလည္​ရင္​ free falling ပုစၥာကို တြက္​လို႔ရၿပီ။ပံု​ေသနည္​းကိုလည္​း ဒီလိုတစ္​ခါတည္​းျပင္​လိုက္​မယ္​။ ၁- a ​ေတြကို g လို႔ျပင္​မယ္​ (အတက္​အဆင္​း နွစ္​ခုအတြက္​ +g,-g ရယ္​လို႔ နွစ္​မ်ိဳး ရွိတယ္​) ၂-အကြာအ​ေဝး s ကို အျမင္​့ h လို႔ျပင္​မယ္​ (သ​ေကၤတ စာလံုး​ေျပာင္​းသြားတာ ဘာမွမဟုတ္​ဘူး)
ဒီ​ေတာ့ ပုစၥာကို​ေသခ်ာဖတ္​ တက္​တာလား၊ က်တာလား။ဖတ္​ၿပီး တစ္​ခါတည္​း အ​ေပါင္​းအနႈတ္​ခြဲ....ဟုတ္​လား။ နာက္​တစ္​ခုက ဖတ္​စာအုပ္​ထဲမွာ free-falling ပုစၥာအတြက္​ ဆိုတဲ့ အီ​ေကြးရွင္​း​ေတြ ထက္​တိုးလာတယ္​။ အီ​ေကြးရွင္​းမ်ားလွတယ္​ ဆိုၿပီး လန္​႔မသြားနဲ႔.....အထက္​က အီ​ေကြးရွင္​း​ေတြကို ျပင္​လိုက္​တာဆိုပါ​ေတာ့.... ဆိုတာ ​ေအာက္​ကိုက်လာတဲ့ ​ေကာင္​​ေတြအတြက္​ ဆိုတဲ့ အီ​ေကြးရွင္​းကို ျပင္​တာ။ ​ေအာက္​ကိုက်လာရင္​ က သုညကိုး။ သုည အစားသြင္​းလိုက္​​ေတာ့ ကိုရတာ​ေပါ့။ ဆိုလဲ အဲ့လိုပဲ....​ေအာက္​ကိုက်လာတဲ့​ေကာင္​​ေတြ အတြက္​